Symmetrisk matris

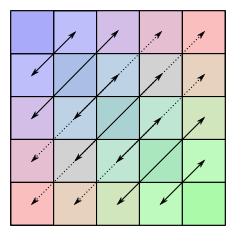
En symmetrisk matris är inom linjär algebra, en matris sådan att den är identisk med sitt transponat:

Om matrisen har elementen a_ij är a_ij = a_ji för en symmetrisk matris. Man kan också uttrycka detta som att rad k i en symmetrisk matris har samma element, i samma ordning, som kolonn k.

${\displaystyle M={\begin{pmatrix}1&2&3\\2&4&5\\3&5&6\end{pmatrix}}}$

M är symmetrisk, eftersom M^T = M.

A nedan är dock inte symmetrisk, vilket man kan se genom att jämföra elementen i A med elementen i A:s transponat, A^T:

${\displaystyle A={\begin{pmatrix}1&2&2\\3&4&5\\3&1&6\end{pmatrix}},~~A^{T}={\begin{pmatrix}1&3&3\\2&4&1\\2&5&6\end{pmatrix}},~~A\neq A^{T}.}$

Symmetriska matriser har alltid en ortonormerad bas av egenvektorer, enligt spektralsatsen, vilket innebär att om A är symmetrisk kan A diagonaliseras med en ortogonalmatris, det vill säga, det finns en diagonalmatris D och en ortogonalmatris T sådan att

${\displaystyle A=T\,D\,T^{T}}$.

där elementen i D:s diagonal är A:s egenvärden.

Om A är en reell matris så är matrisen A^TA symmetrisk, om matrismultiplikationen är tillåten. Detta kan visas med hjälp av räknereglerna för transponat:

${\displaystyle (A^{T}A)^{T}=(A)^{T}(A^{T})^{T}=A^{T}A}$

En symmetrisk linjär avbildning är en avbildning ${\displaystyle F}$ sådan att

${\displaystyle \mathbf {u} \cdot F(\mathbf {v} )=\mathbf {v} \cdot F(\mathbf {u} )}$

för alla reella vektorer u och v. I en ortonormerad bas motsvarar en symmetrisk avbildning en symmetrisk matris på ett entydigt sätt. För att bevisa detta noteras att skalärprodukten i en sådan bas kan skrivas på matrisformen

${\displaystyle \mathbf {u} \cdot \mathbf {v} =u^{T}v,}$

där u och v är kolonnmatriser. Om avbildningen ${\displaystyle F}$ representeras av matrisen ${\displaystyle A}$ i den givna basen kan definitionen skrivas som

${\displaystyle u^{T}Av=v^{T}Au.}$

Om ${\displaystyle A=A^{T}}$ blir transponatet av vänsterledet lika med högerledet. Eftersom vänsterledet är en 1x1-matris är den lika med sitt transponat, så ${\displaystyle F}$ är symmetrisk. Om man utgår från att ${\displaystyle F}$ är symmetrisk får man på samma sätt att

${\displaystyle v^{T}Au=v^{T}A^{T}u'}$

och om detta ska gälla för alla u och v måste

${\displaystyle A=A^{T}.}$

• Hermitesk matris
• Normal matris

v • r Linjär algebra Grundläggande begrepp Skalär · Vektor · Noll · Ortogonalitet · Ekvationssystem · Rum · Linjärkombination · Inre produkt · Oberoende · Bas · Radrum · Kolonnrum · Nollrum · Gram-Schimdt · Egenvärde · Hölje · Linjäritet Linjär algebra Kryssprodukt · Trippelprodukt Matriser Elementär · Block · Enhet · Determinant · Norm · Rang · Transformation · Rotation · Invers · Cramers regel · Trappstegsform · Spår · Transponat · Gausselimination · Symmetri · Addition Multilinjär algebra Geometrisk algebra · Yttre algebra · Bivektor · Multivektor · Tensor Konstruktioner Delrum · Dualrum · Funktionsrum · Kvotrum · Tensorprodukt Numerik Flyttal · Gles matris Kategori