Tesserakt

I världen av Tesserakt hittar vi en mängd olika aspekter och singulariteter som förtjänar att utforskas och förstås. Från dess ursprung till dess relevans idag har Tesserakt varit föremål för intresse och studier av experter och forskare. Mångfalden av åsikter och förhållningssätt om Tesserakt inbjuder oss att reflektera över dess inverkan på olika sfärer i samhället. Genom historien har Tesserakt genererat debatter, kontroverser och till och med inspiration, och satt sin prägel på kultur, vetenskap, politik och andra områden. I den här artikeln kommer vi att fördjupa oss i det fascinerande universum Tesserakt, och undersöka dess många aspekter och betydelse i den samtida världen.

 Den här artikeln behöver källhänvisningar för att kunna verifieras. (2016-10)
Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.
Tesserakt
TypEn tvådimensionell illustration av en regelbunden fyrdimensionell polytop
Celler8 kuber
Sidor24 kvadrater
Kanter32
Hörn16
Hörnformtetraeder
Schläfli-symbol{4,3,3}
Dual16-cell
En tvådimensionell illustration av tesserakt.

En tesserakt, eller 8-cell är en tänkt fyrdimensionell kropp och en av sex regelbundna fyrdimensionella polytoper. Det är den fyrdimensionella representationen av en hyperkub. Tesserakten är ett objekt som är analogen till den tvådimensionella kvadraten och den tredimensionella kuben, det vill säga alla kanter är lika långa, och vinkeln mellan två godtyckliga sidor eller kanter är 90°.

En tesserakt kan visualiseras i tre dimensioner på motsvarande sätt som en tredimensionell kan visualiseras i ett tvådimensionellt plan.

Tesserakten har 8 kuber som sidokroppar, 24 kvadrater som sidor, 32 kanter och 16 fyrtaliga hörn.

Att skapa en tesserakt

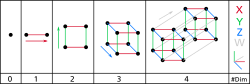
En tvådimensionell avbild av skapandet av en tesserakt.

Alla hyperkuber kan skapas på följande sätt:

  • 1 dimension: två punkter A och B kan bindas samman till en linje AB.
  • 2 dimensioner: två linjer AB och CD kan bindas samman till en kvadrat ABCD.
  • 3 dimensioner: två kvadrater ABCD och EFGH kan bindas samman till en kub ABCDEFGH.
  • 4 dimensioner: två kuber ABCDEFGH och IJKLMNOP kan bindas samman till en tesserakt ABCDEFGHIJKLMNOP.

I samtliga steg är de nya linjerna som skapas alltid vinkelräta mot de gamla, fast i en ny dimension.

Externa länkar