Fermi–Dirac-statistik

Fermi-Dirac-statistik, uppkallad efter fysikerna Enrico Fermi och Paul Dirac, är en sannolikhetsfördelning för ett stort antal identiska fermioner, med tillämpning inom främst fasta tillståndets fysik. Till skillnad från Bose–Einstein-statistik innebär Paulis uteslutningsprincip, att högst ett objekt får finnas i varje kvanttillstånd. Fördelningen kan tillämpas på exempelvis protoner, neutroner och elektroner. Fermi och Dirac härledde fördelningen oberoende av varandra 1926.^[1]

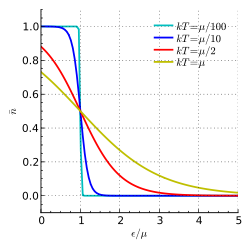
Den används främst för att beskriva elektroner i fasta kroppar tillhörande valens- och ledningsbanden, med energitillstånd som funktion av temperaturen. Sannolikheten n(ε) för att en fermion befinner sig i ett kvanttillstånd med energin ε vid temperaturen T kan tecknas

n(\varepsilon )={1 \over {e^{(\varepsilon -\mu )/kT}+1}}

där

\ \varepsilon

är den aktuella energinivån

\ \mu

är den kemiska potentialen

\ k

är Boltzmanns konstant

\ T

är temperaturen

Vid temperaturer nära absoluta nollpunkten är för varje energinivå $\ \varepsilon <\mu$ sannolikheten nära 1 för att energinivån är besatt. Vid låga temperaturer ( $kT\ll \mu$ ) är $\ \mu$ lika med Ferminivån.

Se även

Källor

William Feller, An Introduction to Probability Theory and its Applications, John Wiley & Sons, New York 1950.
Eugen Merzbacher, Quantum Mechanics, John Wiley & Sons, Toppan Company, New York 1961.
R.E. Peierls, Quantum Theory of Solids, Clarendon Press, Oxford 1955.

Noter

^ Pais, Abraham (1988). Inward Bound – Of Matter and Forces in the Physical World. Oxford University Press. sid. 255. ISBN 978-0-19-851997-3

[1] Pais, Abraham (1988). Inward Bound – Of Matter and Forces in the Physical World. Oxford University Press. sid. 255. ISBN 978-0-19-851997-3

[1]